
Cloudylabs
On peut considérer un muon comme un électron massif et instable. C’est une particule élémentaire avec une masse de 207 me=105,7 MeV/c² et une demi-vie de 2,2 μs (dans son référentiel de repos).
Les muons proviennent de la désintégration des kaons et des pions ces derniers étant produits lors de l’interaction du rayonnement cosmique primaire avec les noyaux de l’atmosphère.
Dans la matière, les muons se comportent comme les électrons, à ceci prés que les pertes par Bremsstrahlung sont 104 fois moins importante par rapport aux électrons, l’énergie critique dans l’air est donc de 1115 GeV alors qu’elle n’est que de 100 MeV pour les électrons.
Les muons (ainsi que les électrons, les taus et les neutrinos) sont des leptons, des particules élémentaires qui ne sont soumis qu’à l’interaction faible, à la force électromagnétique (pour les particules chargées) et à la gravitation.Les muons se désintègrent en électrons ou positons :
Les électrons produits peuvent avoir une énergie variable, en moyenne une trentaine de MeV comme expliqué ici. The end of range of μ- in nuclear emulsion is pictured here.
Les leptons ne sont pas soumis à l’interaction forte car ils ne sont pas composés de quark, et par conséquent ils ne feront (presque) jamais d’interactions avec les hadrons. Un hadron est un assemblage de quark régi par l’interaction forte. Les hadrons les plus connus sont les neutrons et protons (constitué chacun de 3 quarks distinct) qui composent les nucléons d’un noyau. Les nucléons sont maintenus en cohésion dans le noyau grâce à l’interaction forte qui agit grâce à(notamment) l’échange de pion virtuel entre les nucléons. Comme les leptons ne sont pas eux même soumis à l’interaction forte, l’interaction avec les hadrons se fera uniquement via la force électromagnétique commune à toutes les particules chargées. Les muons et électrons ne pourront être que diffusé électrostatiquement par un noyau, mais ils ne pourront pas transférer d’énergie à des hadrons : ainsi un lepton ne fera jamais de « Stars » dans une chambre à brouillard (il est cependant possible à haute énergie qu’un muon puisse rayonner un photon virtuel capable d’interagir directement avec des hadrons en formant des résonances). Cela explique pourquoi des muons rapide peuvent traverser des épaisseurs de plomb importante sans être absorbé : ils ne creent pas de désintégration ni ne sont déviés fortement par des noyaux. A picture : imagine that to the muon, a nucleus appears as a transparent cloud of electricity through which it can pass freely. In the case of strongly-interacting particles on the other hand (π), the nucleus appears opaque; and thus nuclear capture becomes probable.
Perte d’énergie des muons dans la matière
La perte d’énergie linéique totale des muons dans la matière peut s’écrire comme suit :
a correspond aux pertes collisionnel avec les électrons atomique du milieu
b correspond aux pertes radiatives qui comprennent :
- b brems : les pertes par Bremsstrahlung,
- b pair : Les pertes par création de paire (un muon peut rayonner un photon virtuel dans le champ coulombien d’un atome qui se converti en une pair réel électron-positon),
- b nuc : Les pertes par réaction photonucléaire qui correspondent à la photo-absorption par un noyau d’un photon virtuel rayonné par le muon, ce qui s’accompagne d’une profonde excitation de la cible qui peut émettre des hadrons (Pions par ex)
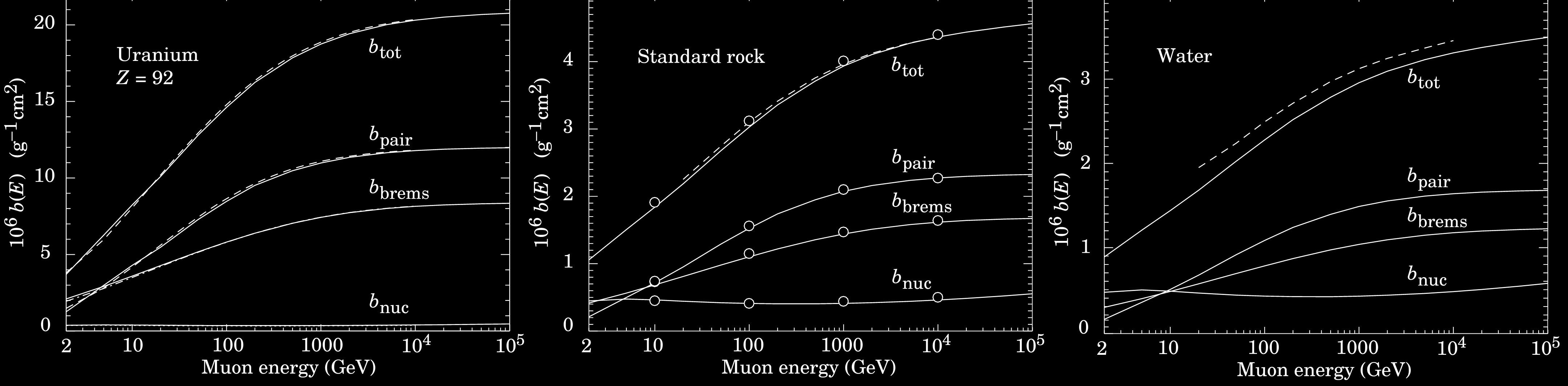
On peut préciser par rapport à l’équation précédente que le terme b(E)E représente moins de 1% de la valeur de a(E) pour des énergies inférieur à 100 GeV et ce pour la plupart des matériaux. Les courbes suivantes montrent la prépondérance des 3 effets radiatifs dans des matériaux de différent Z (pour les roches, Z=11).
La courbe suivante représente l’ensemble des pertes d’énergie des muons dans du cuivre.
On constate que les pertes radiatives ne deviennent prépondérantes que pour des énergies cinétiques très élevée, soit 315 GeV pour le cuivre (1115 GeV dans l’air, 134 GeV dans le plomb). On retrouve le domaine des pertes d’énergie proportionnel à ~ 1/v² (courbe de Bethe) pour la gamme d’énergie [0,1 ; 100MeV].
Les pions π à l’inverse, interagissent fortement avec les noyaux. Les pions sont produits lors des désintégrations (stars). Lorsque les pions ont perdus toutes leurs énergie cinétique et s’arrêtent dans la matière, ils se désintégrent en muons ayant une énergie d’environ 4 MeV.
μ desintégration

The last picture at right, is similar to the event that I recorded in one of my cloud chamber :
At A, the muon is coming up to down and reach the point B where it encounter a nucleus (electrostatic collision) which deflect it a bit to the point C. The path B to C is erratic, this not a straight line like A to B, because during the collision, the muon lose a lot of its kinetic energy. It come at rest at C where it decay into an electron and a neutrino. But due to the large rest mass of the muon (105 MeV/c²), a lot of energy is shared between this 2 particles. After the decay of the muon, the electron can get from 0 to 70 MeV of kinetic energy, but on average, it’s 35 MeV and the rest for the neutrino (see the graph just below). What are we observing ? this is indeed the case. The track C-D is an electron with a very big energy as it’s a straight line, showing no disturbance (deflection). At 35 MeV, the range in air is about 100 meters. How are we sure it can be the disintegration of muon, and not the backscattering of a particle coming from D to C with a collision at C ? because after this process, it’s very unlikely that the line B - A would be straight. It should be erratic, with a lot of deflection due to Coulomb interaction as the particle have literaly no kinetic energy left. So the initial particle, is coming from A.
The end of the muon track (A to C) is similar to the pictures recorded in emulsions, showing the end of muon tracks.
I would like to paste the answer to a comment :
I’d like to know why the nucleus in the point B is not accelerated enough to show an ionized track in the chamber after the electrostatic collision with the muon. Is that because the collision wasn’t close enough? Joaquín Consider the mass of the muon (105 MeV/c²) and let’s consider at B it’s a nitrogen nucleus (71% of air so it’s likely). Nitrogen have a mass of 14 u so 13 132 MeV/c², (MeV/c² come from E= mc² so m=E/c² with E in MeV and u is the atomic mass Nitrogen is 14u). So the mass ratio is 13132/105 = 125. Considering the equation at : https://www.cloudylabs.fr/wp/les-processus-de-pertes-denergie-des-particules/#brem , this give that during the collision, the muon transfer roughly 3% of its kinetic energy to the Nitrogen nucleus. You can do the experiment at home conserving the same ratio of mass, that’s to say, if you throw a ping pong ball (2,7 gram) to a static handball ball (400 grs), the handball won’t move a lot unless you give your pingpong ball a great incoming energy ! Things change a lot if the static mass is similar to the mass of the projectile (2 ping pong ball colliding each other, you will see easily the recoiling one even if the projectile have few kinetic energy ).
What could be the initial kinetic energy of the muon ? without a magnetic field, it’s impossible to know it, but according to this https://www.cloudylabs.fr/wp/wp-content/uploads/2014/01/Range_muon1.jpg it’s acceptable to say that it’s energy is far below 10 MeV as the path A B is not perfectly straight as the muon undergo some electrostatic deflection (this indicate it have few energy). Remember that when the muon comes in the chamber, it loses some energy when it passes through the walls of the room and building. Range of such muon with 10 MeV is still 7 meter in air. So 3% of 10 MeV would give 300 keV to the nitrogen nucleus. What will be the length of the track of the recoiling N nucleus ? I did the estimate with 560 keV energy from a previous experiment : http://www.cloudylabs.fr/wp/rough-identification-of-a-recoil-nucleus/ so the recoil track would be 2 mm. But we don’t observe this recoiling track. Are we sure of that ? no, because if you look to the point B, on the right end of the track, there is a tiny burst of ionisation. It could be the recoiling nucleus, but it receive so few kinetic energy that it move only about hundred of micrometers. This is still an ion, and the vapor can condense on it, making the tiny cloud. If the muon was of great energy, we should have see a recoiling track, exactly like the alpha experiment from https://www.cloudylabs.fr/wp/les-processus-de-pertes-denergie-des-particules/#brem
μ- capture by nucleus (illustrated in nuclear photographic emulsions)
From Powell, 1952, The Study of Elementary Particles by the Photographic Method.
In the early of 1940, it was pictured that when a positive μ is brought to rest to rest in matter (by losing all it’s kinetic energy into ionization), it is prevented from approaching a nucleus, as a result of the Coulomb repulsion between identical charges, and remains free until the instant of its decay. On the other hand, the electrostatic forces will lead to the capture of negative particles by atoms into states of high quantum number and thus forming a ‘muonic atom’. By analogy with electron it was believed that the muon (and the pion) then fall to state of low energy round the nucleus, the transitions being accompanied by the emission of radiation or Auger electrons. In order to confirm the view that the μ- particles do indeed interact with nuclei when arrested in solid substances, and before they had time to decay, experiments were made in which the particles of different charge were separated from one another by magnetic fields, so that the properties of the two types could be separately studied. When brought to rest in iron, it was found, in accordance with expectation, that the positive muons, but not the negative, decay with the emission of a charged particle. In material of low atomic number (graphite, aluminium…), a large proportion of the negative muon decay before interacting with a nucleus.
Left picture : The events, due to capture of a negative muon, were recorded in photographic emulsion plate manufactured underground at a depth of about 40 metres of water equivalent. They were left at this depth for several months; and then processed without being brought to the surface. In such plates, the number of muon arrested in the emulsion is very much greater than the number of pions π. Thus only five positive π particles were observed and identified in the characteristic π-μ decay, in comparison with 1014 muons. In addition, 30 examples were found of negative muon which produced disintegrations (in point p). The two examples represent typical disintegrations with one secondary charged particle, most of which are certainly due to the nuclear capture of μ- by the heavier elements (Ag, Br) in the emulsion. The particle emitted at P are protons, possibly deuterons or alpha particles.
In 1953, MORINAGA and FRY scrutinised the tracks of 24 000 μ- ending in the emulsion and found that 591 of them (2,4%) produced visible disintegrations (see the graph, left below). The μ- were formed by the decay in flight of π- generated in a synchro-cyclotron. They determined the distribution of energy of the secondary protons and α-particles and found a mean value of ~15 MeV, corresponded to that expected for the moderate excitation of a silver or bromine nucleus, value ~25 MeV being uncommon.
Many of the ‘two-prong’ stars represent the emission of a fast proton and the recoiling residual nucleus, the two tracks being widely different in range. Most of such events must be attributed to capture by a light element, for the energy of recoil of a silver or bromine nucleus is too small to produce a recognizable track. In addition to the charged particles, neutron are also produced by the nuclear capture of μ- . Experiments made with counters at depths underground (20 m of water equivalent) indicate that there are between one and two neutron per disintegration, according to the type of nucleus capturing the muon. The above result indicate that only a small fraction of the energy available by the disappearance of the rest mass of the μ- (105,7 MeV/c²) appears among the nucleons of the nucleus which it disintegrates. The reaction is μ-+p → n0+νμ where νμ is a neutrino. The average energy of the neutron is about 20 MeV, most of the available energy is then taken by the neutrino. If the neutron is ejected from a parent nucleus without interacting with another nucleon, no visible disintegration is produced.
To summarize, when a muon reaches the lowest quantum state of a muonic atom, it can decay or be captured on a bound proton. Except for very light nuclei this capture is far more likely than decay. When muon capture occurs in any nucleus, the energy release of about 100 MeV is mainly donated to the neutrino, but the nucleus can and does absorb substantial energy, thus many reactions occur (the nucleus even recoil and get about few MeV of kinetic enrgy) . Example with 28Si . In the ground state of muonic silicon, the muon will decay 34% of the time and capture on the nucleus 66% of the time. Thus, symbolically μ-+28Si → 28Al*+νμ (* mean the nucleus is excited). Of those captures, about 36% will produce no neutrons, 49% will produce 1 neutron, 14% will produce 2 neutrons and 1% will produce 3 neutrons. The main mechanism of de-excitation after muon capture is neutron emission, but charged particles can also be emitted. However, this is a minor component of the capture process : protons, deuterons and alphas which are emitted are typically low energy (2-20 MeV) and thus have a short range. More about muon capture.
Auger Electron from the μ- capture by nucleus
We can complete the process of negative muon capture by a nucleus with the observation, in photographic nuclear emulsion, of Auger electron. When a negative muon stops in a material, it quickly becomes attached to an atom that form a muonic atom. In a muonic atom, an electron is replaced by a muon, which, like the electron, is a lepton. All this process is accomplished in a period about 10-13 s, a time short compared to the mean lifetime of a muon. For example muonic hydrogen atoms are much smaller than typical hydrogen atoms because the much larger mass of the muon gives it a much more localized ground-state wavefunction than is observed for the electron. In multi-electron atoms, when only one of the electrons is replaced by a muon, the size of the atom continues to be determined by the other electrons, and the atomic size is nearly unchanged. However, in such cases the orbital of the muon continues to be smaller and far closer to the nucleus than the atomic orbitals of the electrons. The muonic atom freshly formed is highly excited, and a part of the energy of desexcitation can be transferred to atomic electrons that we can see in nuclear emulsions. These electron are called Auger electrons.
In nuclear emulsions, it’s possible to observe these Auger electrons if their energy is not too low. A 15 keV electron form a very short track, very difficult to discriminate in an emulsion. The energy of Auger electrons increase with the Z of the atom. For light elements, the Auger process is much more probable than the radiative one, but most of the Auger electron have an energy less than 15 keV. For heavy elements like silver and bromine, Auger electrons have energy between 15 and 75 keV so they are easily recognizable in an emulsion. This behavior provide a method of distinguishing the disintegrations of light and heavy elements in an emulsion : if no or low energy Auger electron are found in a disintegration, it was a light atom (C,N,O). If Auger electrons are clearly presents (long track), it was a heavy atom (Ag, Br, I) which disintegrated by the muon capture. Similar considerations apply to π- particles.
The most accurate measurements of the relative frequency with which Auger electrons can be distinguished during the capture of μ- by elements in the emulsion were obtained in FRY’s experiments with particles formed by the decay in flight of artificially produced π-. From a total of 1000 μ- observed to stop in the emulsion :
⋅ 358 decayed with the production of a fast electron. Among the 358, 17 showed also slow electrons (observation of the decay electron of μ and Auger electrons due by its capture by a nucleus).
⋅ 32 produced a star,
⋅ 355 had no associated secondary particles,
⋅ 180 showed one slow electron,
⋅ 57 showed two slow electrons,
⋅ 18 showed three slow electrons.
Auger electrons appear with a probability of (180+17) ≥20% when there is a nuclear disintegration
.
Link nội dung: https://liveproject.edu.vn/muon-du-qua-a74837.html